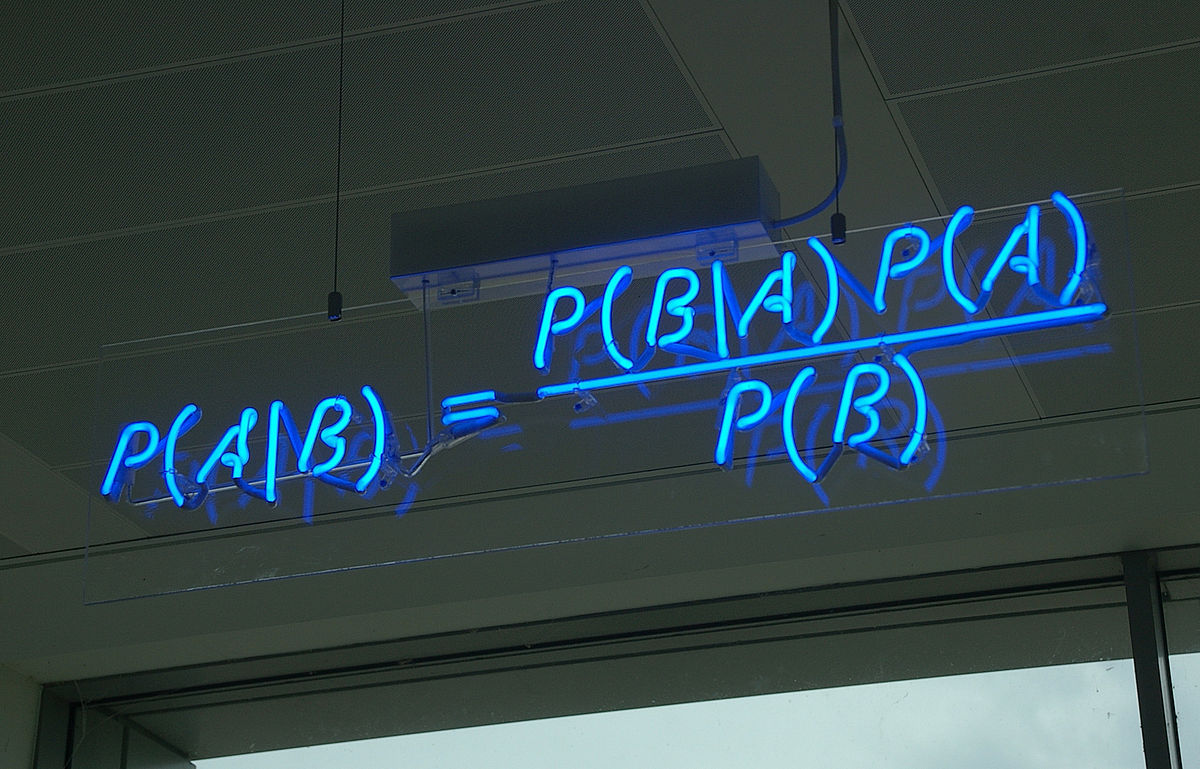The Knapsack problem is one I’ve encountered a handful of times, both in my studies (courses, homework, whatever…), and in real life. Unfortunately, the times I encountered it in a real situation I never had to actually fully solve it – it was more along the lines of, “hey, this is just like the Knapsack problem, but we can work around it”.
I’m currently taking a course on discrete optimization, a field I’ve always thought was cool but never been great at and one which also has a reputation for being particularly hard as you progress deeper. As a way for me to brush up on some basics I thought I’d revisit dynamic programming, an often used technique in solving discrete optimization problems, with the Knapsack problem. The course is very adamant in trying all the different covered algorithms on all problems; for example, if solving Knapsack starts to be too time consuming with DP, use Linear Programming or Branch & Bound with some type of constraint relaxation. To that I say, I will… but I also won’t! I’ll of course try all the algorithms, but since this is a discrete optimization course, I also thought “let me make this even more painful” and try to optimize each algorithm as best I can 🙂
Contents
Introduction
The Knapsack problem is actually a combinatorial optimization problem where we need to find an optimal number of objects from a finite set of objects usually based on their properties. It’s an interesting problem as it is both an NP-hard (optimization) and NP-complete (decision) problem that has a pseudo-polynomial algorithm, meaning its worst-case time complexity is polynomial in numeric values of the input. We’ll go through the problem both informally and formally.
Informal
Imagine you’re at the farmers market with a single bag to carry home your produce. Because there are so many nice things at the market, and your bag only has capacity \(K\), you’ll need to choose very carefully what you want to buy from items in the set \(\mathcal{I}\). So, how do you choose the items? The first approach may be to simply maximize the value in your knapsack by either picking or leaving an item based on their value (i.e, how much they’re worth or how tasty they are). Another approach may be to maximize the value density per item in your bag, since we know how much all the items weigh individually and their value.
As this is post is about solving the 0/1 Knapsack problem, we’ll only be focused on the first possible approach. We want to maximize the total value in our knapsack by either picking or leaving an item.
Formal
0/1 Knapsack means that we solve the problem by restricting an item to either 0 or 1; left or picked, in or out. Given a set of items \(\mathcal{I}\) with weight and value \(w_i, v_i\), and a knapsack with capacity \(K\), we want to maximize the sum of our items value subject to our knapsacks capacity. More formally we can model the problem with ab objective function to maximize, subject to constraints and a decision variable:
Maximize
\(
\large\sum_{i = 1}^\mathcal{I} v_i x_i \\
\)
subject to
\(
\large\sum_{i = 1}^\mathcal{I} w_i x_i \leq K
\)
where \(x_i \in \{0, 1\}\), is the binary decision for each item.
If one ignores the computational cost and inefficiency, the easiest and simplest approach to solving this is by brute force. Following this is a trivial greedy approach, where we can improve it by maybe using a simple heuristic during search, or beforehand. For example, sorting the items by value and choosing one-by-one until we reach capacity \(K\). Here’s a greedy example:
value = 0
weight = 0
knapsack = [0] * len(items)
for i in items:
if weight + item.weight <= capacity:
knapsack[item.index] = 1
value += item.value
weight += item.weight
The issue with a greedy algorithm is that, even after you leave it running for months, the solution it gives has no guarantee of being the best or most optimal one. Proving the solution is correct becomes tricky and you’ll have to spend further time on a proof. Remember, Knapsack is NP-Complete. A better and smarter approach (psst, the hint is in the title) is to use Dynamic Programming!
Dynamic Programming
Dynamic programming (DP) is a technique used when the solution to a problem has an optimal substructure and overlapping sub-problems. At its most basic, it’s a “better version of divide and conquer” – a description which is wrong but gives a very general “layman’s” overview. DP consists of programming in such a way where one uses past knowledge of a problem to solve it. This essentially means that if you take a problem and divide it into smaller and smaller sub-problems, at some point, you’ll be solving the same subproblem again. Because there’s a high likelihood of re-seeing the same subproblem, the results of these sub-problems are memoized; stored for later, ideally in cache. Because we have these sub-problems and their solutions stored, we can now also use them to help us solve bigger problems until we’ve solved our original problem. An example would be calculating the \(n^{\text{th}}\) fibonacci number. If \(n\) is huge, it may take some time… unless you already have the solution to \(f(n – 1, n – 2)\), where \(f\) is a function for calculating a fibonacci number.
Solutions to previous sub-problems in the fibonacci example can be stored in a lookup table, making access time quick and efficient. This fast/low time complexity comes at a cost of having high space complexity from storing all previous results.
It’s a great technique for powerful algorithm design, path-finding problems, and reducing time complexity. It’s also usually one of the first and “easiest” methods of solving discrete optimization problems, given the problem has the appropriate properties. One must also take into account the exact problems constraints and other details of course. My professor once called it “careful bruteforce”. As a side-note, I hate the name.
I’ll briefly cover the Fibonacci sequence with DP as an example before jumping back into Knapsack. Let’s say I want to compute fibonacci to the 10 millionth integer, a computation which is sure to take some time.
A common way of computing fibonacci is by implementing it recursively:
def fib(n):
if n <= 2:
return 1
return fib(n - 1) + fib(n - 2)
Even though the above implementation works, it’s not at all efficient as n gets bigger. Imagine having to recurse \(1000000\) times! Its time complexity is also less than desirable since it is exponential. We can represent fib as an equation, \(T(n-1) + T(n – 2) + \mathcal{O}(1)\), meaning the time to compute for fib(n) is equal to the sum of time taken to calculate fib(n - 1) and fib(n - 2) plus a time constant. This produces an upper bound of \(\mathcal{O}(2^n)\), or more specifically \(\mathcal{O}(2^\phi)\), where \(\phi\) is the golden ratio.
We can now compute the fibonacci series, even though it’s very slow. To make this faster we can implement the same function above using a technique called memoization. The idea of memoization is a simple one as stated earlier, especially for our fib use case. Whenever we compute a number in the sequence, we store it in a “cache type variable” – here, in Python, we use a dictionary. For now, ignore any language or other type optimizations we can do. So when we are computing our fib sequence, we can check our cache variable for numbers that have already been computed removing the need to constantly re-compute them. Let’s rewrite our fib function with this in mind:
mem = {}
def fib(n):
if n <= 2:
return 1
if n in mem:
return mem[n]
mem[n] = fib(n - 1) + fib(n - 2)
return mem[n]
Let’s do a quick time complexity analysis. Any non-memoized calls, i.e, when we call fib(n), costs us \(n\), and any memoized calls costs us \(\mathcal{O}(1)\). This leaves us with \(\mathcal{O}(n)\), which is a huge improvement! Take note how we’re also breaking down our task into smaller little sub-problems by introducing more variables and processes, rather than just one recursive function.
We’ve now got the building blocks to transform this solution into a DP one. DP algorithms are often times referred to, and implemented as bottom-up. When we program recursively, we usually start thinking about how to code it from the “top”, and work our way down. With a bottom-up approach we… well, we do the opposite: we work our way to the top from the bottom. For example, we usually learn maths in a bottom-up approach, but learn sports top-down – play first then get used to the rules. In our code, instead of having the recursive call to fib, we’ll implement a for loop.
def fib(n):
f2 = 0
f1 = 1
if n <= 2:
return 1
for i in range(1, n):
f = f1 + f2
f1, f2 = f, f1
return f
There are more LOC, but, the code is now a more optimized, faster, and efficient solution to our simple fibonacci problem! Note, it’s still \(\mathcal{O}(n)\). If it’s not clear why this is better, we now end up needing only the last two numbers to calculate the next number, as opposed to having to recalculate the entire fibonacci “tree” for each \(n\) (1st solution).
For empiricism, here are run times with all three methods of computing Fibonacci:
- Recursion:
fib(40)– \(\sim\) 21.5s - Memoziation:
fib(250)– 258 µs \(\pm\) 4.88 µs per loop (mean \(\pm\) std. dev. of 7 runs, 10000 loops each) - Bottom-up (DP):
fib(250)– 137 µs \(\pm\) 11.2 µs per loop (mean \(\pm\) std. dev. of 7 runs, 10000 loops each)
0/1 Knapsack
Having gone over the formal formulation of the problem we can now design a solution. The first step is to identify or break the problem down into sub-problems as required for DP algorithms. Let’s assume we have a knapsack with capacity \(K = 8\) and \(4\) items, \(\mathcal{I} = {1, 2, 3, 4}\), each with a weight and value, \(w_i, v_i\). Now, while this is still a very easy problem that you could solve in your head, it may take a minute or two to go through all the combinations of items. What if you \(0\) items? \(1\) item? \(2\) items? You can see that as the items decrease it becomes easier to solve. These are our sub-problems!
If you imagine we have a 2-dimensional matrix or tensor, of size \(O(\mathcal{I} + 1, K + 1, )\) where each row x column pair is a sub-problem solution, we can use this to solve a complete Knapsack problem. Take as an example item 1, \(i_1\), with properties \(w_1 = 8. v_1 = 80\). With capacity \(K\), our matrix would start to look like this:
\(
\begin{array}{c|lcr}
i & \text{0} & \text{1} & \text{2} & \text{3} & \text{4} & \text{5} & \text{6} & \text{7} & \text{8} \\
\hline
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 80
\end{array}
\)
Remember the first row is for item \(0\) (no items), and the first column is with capacity \(0\). So, with this format of DP set in place, we’re now looking for the optimal value solution \(O(i, K)\).
To continue filling up the DP matrix, we need to define a recurrence relation. This is an equation that recursively defines a sequence of values in an array, which our matrix rows and columns are. Specifically, we will be using the Bellman equation. Completing the 3rd row of our matrix with \(i_2\) having \(w_2 = 5, v_2 = 40\) we get:
\(
\begin{array}{c|lcr}
i & \text{0} & \text{1} & \text{2} & \text{3} & \text{4} & \text{5} & \text{6} & \text{7} & \text{8} \\
\hline
2 & 0 & 0 & 0 & 0 & 0 & 40 & 40 & 40 & ?
\end{array}
\)
What happens with \(O(2, 8)\)? We can see that the clearly optimal solution would be to take \(i_1\) as its value is double the current items but what if we didn’t? How is this decision made? This is where the recurrence relation comes in and defines the rules for “traversing” and filling the table until the problem is complete. At each \(O(i, K)\) we check the item’s weight against the knapsack capacity. If \(w_i \leq K\) then we either choose \(O(i – 1, K)\) or \(O(i – 1, K – w_i) + v_i\). Since we’re optimizing our carrying capacity in the knapsack, we choose the maximum of those two values. Let’s use this to fill the rest of our matrix where \(w_3 = 3, v_3 = 20\) and \(w_4 = 1, v_4 = 50\).
\(
\begin{array}{c|lcr}
i & \text{0} & \text{1} & \text{2} & \text{3} & \text{4} & \text{5} & \text{6} & \text{7} & \text{8} \\
\hline
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 80 \\
2 & 0 & 0 & 0 & 0 & 0 & 40 & 40 & 40 & 80 \\
3 & 0 & 0 & 0 & 20 & 20 & 40 & 40 & 40 & 80 \\
4 & 0 & 50 & 50 & 50 & 70 & 70 & 90 & 90 & 90
\end{array}
\)
Our optimal value is \(90\) by choosing items \(i_3, i_4\).
To formalize this, we end up with:
\(
O(i, K) = \max{(O(i – 1, K), O(i – 1, K – w_i) + v_i)} \\ \quad \text{if } w_i \leq K \\ \quad \text{otherwise } O(i – 1, K)
\)
which is a slight variation of the Bellman equation.
One last thing to touch upon is how we actually find out what items we’ve chosen. In order to traceback through the matrix and find which items have been selected, we end up doing a similar reverse operation starting from \(O(i, K)\):
- If \(O(i, K) != O(i – 1, K)\)
- \(i\) is a chosen item and is marked as taken, \(1\)
- Move to \(O(i – 1, K – w_i)\)
- If \(O(i, K) = O(i – 1, K)\)
- \(i\) is not chosen and is marked as such, \(0\)
- Move to \(O(i – 1, K)\)
Once this is over, we’ll have a) an optimal value and, b) array of values to take and leave. Following this algorithm for our matrix gives us an array \([0, 1, 0, 1]\)
Implementation
Implementing this in Python is very straight forward if the steps highlighted above are followed. Since we’re filling out a matrix we need two for loops. One for the rows and one for the columns. Inside these loops we use our recurrence relation.
def dp(item_count: int, capacity: int, items: list):
table = np.zeros((item_count + 1, capacity + 1), dtype = np.int32)
for i in range(item_count):
for w in range(capacity + 1):
if items[i].weight <= w:
p1 = table[i][w]
p2 = items[i].value + table[i][w - items[i].weight]
table[i + 1][w] = max(p1, p2)
else:
table[i + 1][w] = table[i][w]
...
Items = namedtuple("Item", ["value", "weight"])
items = [Item(80, 8)]
Some things to note:
itemsis a list ofnamedtuplesso that it contains value and weight attributes for each item- Since the first row of the matrix is going to be empty and contain only \(0\), I use
i + 1asiandiasi - 1. This is important to remember when reading the code. Of course, it can be done in other ways but ¯\_(ツ)_/¯ - This is sloooooow.
We now need to implement the traceback discussed above.
knapsack = []
knapsack_opt_val = table[item_count][capacity] # [-1][-1]
w = capacity
for i in range(item_count, 0, -1):
if table[i][w] != table[i - 1][w]:
knapsack.append(1)
w -= items[i - 1].weight
i -= 1
else:
knapsack.append(0)
return(knapsack_opt_val, knapsack)
More things to note:
- Again, there are different ways to implement this loop, like pre-allocating an array
knapsackneeds to be reversed at the end since our first item is \(O(i, K)\) ->knapsack.reverse()
We can now produce an optimal knapsack solution and retrieve the chosen items!
Optimization
This to me was the most fun part of the problem. Technically we have a working solution. It takes roughly 15 seconds to compute a solution for 40 items, and 1 minute 30 for 50 items. Clearly this isn’t going to work when we have 200 items.
Taking a step back, our current algorithm has time complexity \(\mathcal{O}(Kn)\), where \(K\) is the size of the knapsack and \(n\) is the number of items – our two for loops. However, one needs to take into account multiple things:
- Python can be slow (fight me)
- \(K\) needs \(\log{K}\) bits to be represented
- This actually makes our \(\mathcal{O}(Kn)\) exponential in the size of the input, hence being pseudo-polynomial, something I mentioned earlier
To optimize this you might say, “just rewrite it using C++” or something similar right? Right, well, I’ve done that, but, there are also a lot of optimizations that can be done directly in Python to both the algorithm and Python itself. I actually ended up spending about 15 days optimizing everything (way too much), but it was very fun and I learnt a lot, especially when vectorizing the code, something I’ve done maybe only once as an exercise.
Space optimization
The first optimization we can do actually involves approaching the DP problem differently. In the specifics of Knapsack, if you pay attention to the problem formulation and the code (in other words, what we’re actually doing), you can see that we’re only ever using rows i and i + 1. This means we don’t need \(i\) rows in our matrix. We only need 2! This will reduce our matrix space from \(O(i, K)\) to \(O(2, K)\).
Doing this however means we cant use i inside our loops when accessing the matrix as we’ll be out of bounds. We only need to loop between 0 and 1. One way to achieve this is by using some simple bitwise manipulation. If we AND (&) the value of i with 1 we’ll always get back either 0 or 1, allowing us to access both rows of the matrix.
...
for i in range(item_count):
c, p = (i & 1), (~i & 1)
for w in range(capacity + 1):
if items[i].weight <= w:
p1 = table_small[c, w]
p2 = items[i].value + table_small[c, w - items[i].weight]
table_small[p, w] = max(p1, p2)
else:
table_small[p, w] = table_small[c, w]
...
c and p are the equivalent of i and i + 1. p1 here is the current row and p2 is the current row minus the item’s weight but with the addition of item[i].valueas per the Knapsack formulation (\(O(i – 1, K – w_i) + v_i\)). If the condtional statement is False, we simply assign the current row to the previous row. It’s important to remember that we’re not really incrementing and iterating over the matrix with c and p as we would with i, they’ll always be alternating between 0 and 1 respectively.
We’ve now improved space complexity and got a slight decrease in run time. Howver, the downside of this is that can no longer traceback through the matrix and find the knapsacks items. It’s worthwhile noting that you can also reduce using 2 rows to just using 1 but I didn’t bother with this.
Binary matrix
Another space saving optimization is to convert the matrix from np.int32 to np.bool. We essentially only store decisions at each \(O(i, K)\) hugely decreasing the size of the matrix in RAM. To do this we’ll need to compute the DP matrix as normal, only with 2 rows however, but we also compute a binary matrix and store \(O(i, \mathcal{K}) != O(i – 1, K)\) as a decision variable. \(O(i, K)\) will be \(1\) if its value isn’t the same as the one above it, which will either be the current item or the \(O(i – 1, K – w_i)\), otherwise it will be \(0\).
def dp_opt_v2(item_count: int, capacity: int, items: list):
table_small = np.zeros((2, capacity + 1), dtype = np.int32)
table = np.zeros((item_count + 1, capacity + 1), dtype = np.bool)
for i in range(item_count):
c, p = (i & 1), (~i & 1)
for w in range(capacity + 1):
if items[i].weight <= w:
p1 = table_small[c, w]
p2 = items[i].value + table_small[c, w - items[i].weight]
table_small[p, w] = max(p1, p2)
table[i + 1, w] = int(table_small[c, w] != table_small[p, w])
else:
table_small[p, w] = table_small[c, w]
table[i + 1, w] = 0
Note I’m also using the 2 row matrix optimization alongside this so it is still possible to retrieve the optimal solution, otherwise we would be able to traceback but not have an actual solution… although there are other ways to derive it from this, such as using the knapsack array, but alas, tomato potato.
This optimization also requires a slight modification of the traceback algorithm. We now need to look at if \(O(i, K) = 1\). If it does, this item was chosen, otherwise it wasn’t.
knapsack = []
knapsack_opt_val = table_small[-1][-1]
w = capacity
for i in range(item_count, 0, -1):
if table[i, w] == 1:
knapsack.append(1)
w -= items[i - 1].weight
i -= 1
else:
knapsack.append(0)
return (knapsack_opt_val, knapsack)
We’ve now got a solution which encompasses a binary matrix to traceback and find the knapsack’s items and we only use a \(O(2, K)\) matrix to store the optimal solution instead \(O(\mathcal{I}, K)\). This has saved us some signigicant space complexity, however, the fact is we still have 2 slowfor loops. If only there was a way to speed up even just 1 loop while also using the above optimizations…
Vectorization
This final optimization is the one which took me the most time… many days of trial and error and re-reading numpy documentation and vectorization tutorials. Turns out it was an excellent exercise in doing vectorization (to me anyway, especially since this is my 2nd time?). Fun fact, once I’d finished this optimization using my test data, I tried using it with a real problem, one in the 10s of thousands of items and capacity 1 million. I forgot to change table‘s dtype to np.int32 rather than np.int8 so all my calculations were overflowing. Took me longer than I’d like to admit to figure out my “typo”.
Anyhow, because we’re doing operations on a matrix, and because numpy is being used, one very rewarding and powerful way to speed this up is to use vectorization. Vectorization is the process of rewriting a for loop so that instead of iterating \(K\) times to process our row, in our case, we process the entire row simultaneously. We can do this thanks to vector and SIMD instruction sets in CPUs which can apply the same operation to some data.
numpy has a lot of functions that are vectorized, and so in an ideal world, rewriting code in Python that makes use of these vectorized functions is a matter of finding the right one replacing it with your for loop. Of course, there may be constraints to your particular problem which make vectorization harder or not possible, so it’s not a “magic” spell that works everywhere.
Vectorization tends to work best on problems that require the same operation over and over. Likewise, it’s also simpler to implement on straightforward and simple for loops and ones without too many dependencies such as read-after-write, indirect memory acces or complicated indexing.
As a slightly-oversimplified example, take this loop in C++ and Python:
for (int i = 0; i <= 20; i++)
row[i] += column[i];
for i in range(20):
row[i] += column[i]
A vectorized solution would look like this:
for (int i = 0; i <= 20; i += 4)
row[i:i+3] += column[i:i+3]
row += column
A few things to note besides the simplifications:
- We’re assuming that the Python arrays are actually
numpy.ndarray - Vectorizing in Python with
numpyis different than in C++ where you tell the compiler to vectorize, plus some extra magic numpyalso handles broadcasting- In the C++ vectorized version we’re using 4 because we’re processing 4 elements at the same time
I’ve added some much more detailed information on vectorization in the “Resources & References” section at the bottom.
With that brief in mind, let’s move on to vectorizing our Python code with numpy.
The code we want to vectorize is the 2nd for loop where we iterate over \(K\). Let’s go through exactly what we’re doing in the loop and make a note of all the operations that are actually going on.
if items[i].weight <= w- Assign \(O(i – 1, K)\) and \(O(i – 1, K – w_i)\) to some variables
- Compute \(O(i, K)\)
numpy has a a great function called True and False. As a quick example, if we have an array and want to add \(10\) to all the values greater than some \(n\), np.where would look like this:
array = np.arange(5)
for i in range(len(array)):
if array[i] > 2:
array[i] += 10
array = np.arange(5) array = np.where(array > 2, array + 10, array)
np.where goes through all the elements in array for us without the need for the explicit for loop. Try this exercise also:
- Create two random
numpyarrays of equal length and size - Use
np.whereto check ifarray1\(>\)array2with the outputs1, 0forTrueandFalse
I actually got stuck here for a long time trying to feed it np.where(items[i].weight <= w, ...) or some variation of. Needless to say I couldn’t get this to work as I kept getting tripped up by the prev variable, and more specifically, table[i][w - items[i].weight]. I figured a rewrite of the loop and conditional logic would be required to get this to work… here’s where the pain started! 🙂
I’ll save you the time I spent figuring this out, but we can actually get rid of the if statement and use the current item’s weight from the first for loop to achieve the same thing. We can just do operations on or with table[i, :w_i], table[i, :-w_i], and table[i, w_i:].
table_bool = np.zeros((item_count + 1, capacity + 1), dtype = np.bool) # binary matrix
table_small = np.zeros((2, capacity + 1), dtype = np.int32) # 2 rows to store optimal solution
for i in range(item_count):
w = item[i].weight
c, p = (i & 1), (~i & 1) # go between row 0 & 1 always
table_small[c, :w] = table_small[p, :w]
row1 = table_small[p, w:]
row2 = table_small[c, :-w] + item[i].value
table_small[c, w:] = ...
We’re doing a few crucial and possibly “hard-to-wrap-your-head-around”™ things here with respect to logic, so it’s best to explain with an example during the first iteration of the loop:
- Make row
c(0) equal to rowp(1) up until thewth index (essentially being theifstatement checking for the weight condition, as it let’s us “skip” up until that point)- We’re doing this to essentially “reset” the values that don’t fit in the knapsack during the current iteration
- Notice how we then assign values to
table[c, w:]
- Assign
row1the value of the alternate row (row1) in the iteration from thewth element onwards, wherewis the current item’s weight- We’re only interested in filling in the part of the matrix where the item can actually fit into the knapsack
- Assign
row2the value of the this row (row0) in the current iteration without the last \(w_i\) elements and add \(v_i\) to all of them- This is the equivalent of \(O(i – 1, K – w_i) + v_i\) but in vectorized form
row1 and row2 are the equivalent of our p1 and p2 from other solutions. The majority of the logic comes from understanding the advanced indexing we’re using and the fact that we can operate on all elements of a row in one swift line without the need of a for loop. These ideas, and how arrays are broadcast, are key for understanding this vectorized solution. If you’re struggling to get your head around this, like I did the first too many times, try playing with this in a notebook.
Now we need to compute the current row’s values from the \(i\). To do this we’ll use np.where and compare row1 and row2. This is actually the easiest part. We check if elements in row2 are greater than elements in row1. If an element returns True, we assign row2, \(O(i – 1, K – w_i) + v_i\), else row1, \(O(i – 1, K)\) just as always. Of course this comparison could also be done the other way round.
table_small[c, w:] = np.where(row2 > row1, row2, row1) table_bool[i + 1, w] = np.where(table[c, w:] != table[p, w:], 1, 0)
I’ve also gone ahead and implemented np.where for the boolean/binary matrix to store item decisions and traceback through the knapsack once we’re finished. We already know how to traceback through a binary matrix since we implemented it during the second optimization.
Results
Now that this has been optimized a few times over, we can look at some quick results:
- 4 items, capacity 5 (mean ± std. dev. of 10 runs, 100 loops each):
- Default implementation: 93.1 µs ± 9.58 µs per loop
- Fully optimized: 87.5 µs ± 8.65 µs per loop
- 20 items, capacity 30,000
- Default implementation: 3.47 s ± 257 ms per loop (mean ± std. dev. of 10 runs, 10 loops each)
- Overall 5m 47s
- Fully optimized: 2.26 ms ± 137 µs per loop (mean ± std. dev. of 10 runs, 100 loops each)
- Overall 2.27s
- Default implementation: 3.47 s ± 257 ms per loop (mean ± std. dev. of 10 runs, 10 loops each)
Taking those averages and having a rough estimate, running the 2nd test with 100 loops on the default implementation would’ve taken roughly an hour to complete. That’s almost a speed up of x1500!
I would’ve tested more, but I realllly, couldn’t be bothered to wait so long for things to finish running. Another important note is that while the first two optimizations have very little effect on time, if any, it did greatly help with RAM. I was unable to compute a solution to 10,000 items with 1,000,000 capacity due to the overhead of having a 10,000 x 1,000,000 np.int32 table allocated otherwise.
Full code can be found here: Python, C++.
![]()
Resources & References:
What is vectorization?
Why is vectorization faster in general than for loops?
SIMD examples
Programming guidelines for vectorizing C++
Fundamentals of Parallelism on Intel Architecture
Vectorizing a loop with G++
MathJax reference